题目描述
zdw有一些地毯, 每个地毯分别铺在了[$L_i,R_i$]的区间上
但是zdw的强迫症犯了, 他不想让任何地毯有任何部分重叠(也就是两个区间的交非空)
显然zdw需要移除一些地毯, 但他又希望没有被地毯覆盖的点尽量少
请你帮zdw计算一下, 仅能保留不重叠的地毯时未被覆盖的点最少为多少个?
输入描述
第一行两个整数 $m,n$ 分别表示点的总数(分布在[1,m])和地毯的总数
接下来 $n$ 行每行2个整数 $l_i ,r_i$ 表示第 $i$ 个地毯覆盖的区间范围
输出描述
仅一行, 一个整数, 表示未被覆盖的点的数量最少是多少
具体见样例
样例输入
7 3 1 3 5 7 4 5
样例输出
1
样例描述
一开始的状态如图所示(红,绿,蓝分别对应第1,2,3片地毯)
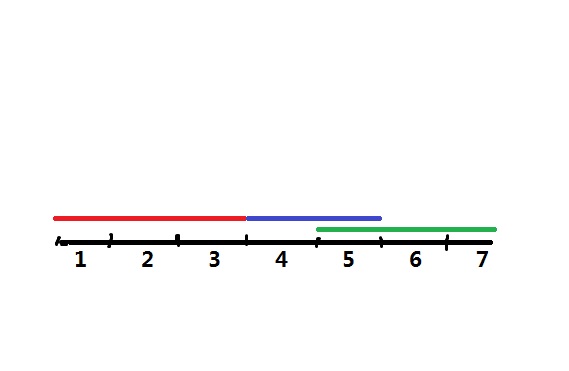
容易发现第 $2$ 片地毯和第 $3$ 片有重叠部分, 所以显然只能选择其中的一个
如果我们选择保留第{$1,2$}片地毯, 显然 $4$ 号点未被覆盖
如果我们选择保留第{$1,3$}片地毯, 显然 $6,7$ 号点未被覆盖
所以显然至少有一个点无法被覆盖, 故答案为 $1$
数据范围
$ m <= 10^{18} $, $ n <= 200000 $
$ 1 <= L_i <= R_i <= m$
子任务1:(10分)
$n <= 10$
子任务2:(10分)
$n <= 20$
子任务3:(40分)
$m <= 2*10^5$
子任务4:(100分)
无其他限制


