题目描述
zdw正在实验室里出题, 然而苍蝇实在是太多了, zdw感到十分烦躁
zdw决定消灭一些苍蝇, 不过他还要出题, 所以只有K次打苍蝇的机会
目前的情况如下:
1. 苍蝇分布在一个二维的平面上, 在 $(x_i,y_i)$ 处有 $z_i$ 只苍蝇
2. zdw可以选择打击 $(x_i,y_i)$ , 此时这一点上的所有苍蝇会被消灭, 但打击点一圈的距离为1的苍蝇会向外移动一步(具体见样例)
3. 请问经过K次打击后, zdw最多可以消灭多少只苍蝇?
输入描述
第一行两个整数 $n,K$ 分别表示苍蝇聚集的位置数和zdw可以打击的次数
接下来 $n$ 行每行3个整数 $x_i ,y_i ,z_i$ 表示在 $(x_i,y_i)$ 处有 $z_i$ 只苍蝇
输出描述
仅一行, 一个整数, 表示zdw最多可以消灭的苍蝇数
样例输入
9 2 1 1 1 1 2 1 1 3 1 2 1 1 2 2 1 2 3 1 3 1 1 3 2 1 3 3 1
样例输出
3
样例描述
一种可行的方案是先打击 $(1,1)$ , 再打击 $(3,3)$
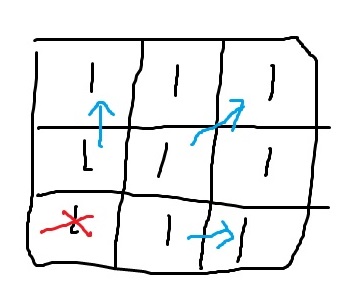
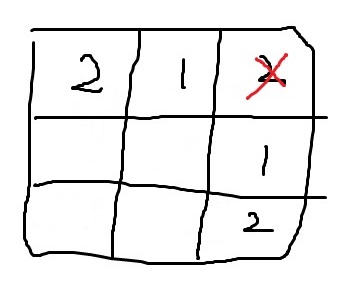
数据范围
$ 0 <= n <= 40000, 0 < K <=3 $
$ 1 <= x_i , y_i, z_i <= 200$
保证对于 $ i \not= j $ 有 $ x_i \not= x_j $ 或 $ y_i \not= y_j $
子任务1:(10分)
$ K = 1 $
子任务2:(20分)
$ 0 <= n <= 9 $
$ 0 < x_i , y_i <= 3$
子任务3:(30分)
$ K = 2 $
子任务4:(40分)
$ 0 <= n <= 900 $
$ 0 < x_i , y_i <= 30$
子任务5:(200分)
无其他限制


