题目描述
平面上有n个信号接收器 $(x_i,y_i)$
zdw计划在 $(0,0)$ 点放置一个无线信号发射器
他想知道如果要让至少m个信号接收器处于发射器的覆盖范围内, 发射器的覆盖半径需要为多大?
这个问题当然很简单辣~ 不幸的是zdw的信号发射器出了点问题, 覆盖范围变成了一个直角的扇形
不过幸运的是zdw还可以调整信号发射器发射的方向, 也就是可以"旋转"扇形的方向
请你帮助他解决这个问题吧
另: 为了方便起见, 你只需要输出发射器的覆盖半径的平方即可
例如半径为 $R$ 则输出 $R * R$ .不难证明 $R * R$ 总可以表示成整数.
输入描述
第一行两个整数 $n,m$ 分别表示信号接收器的总数和要求至少覆盖的接收器个数
接下来 $n$ 行每行2个整数 $x_i ,y_i$ 表示第 $i$ 个信号接收器的坐标
保证不存在两个坐标相同的信号接收器, 且不会有信号接收器位于 $(0,0)$
输出描述
仅一行, 一个整数, 表示发射器的覆盖半径的平方
如果不存在任何合法解, 请输出-1
具体见样例
样例输入
6 4 50 0 12 1 23 7 3 3 1 6 -1 14
样例输出
197
样例描述
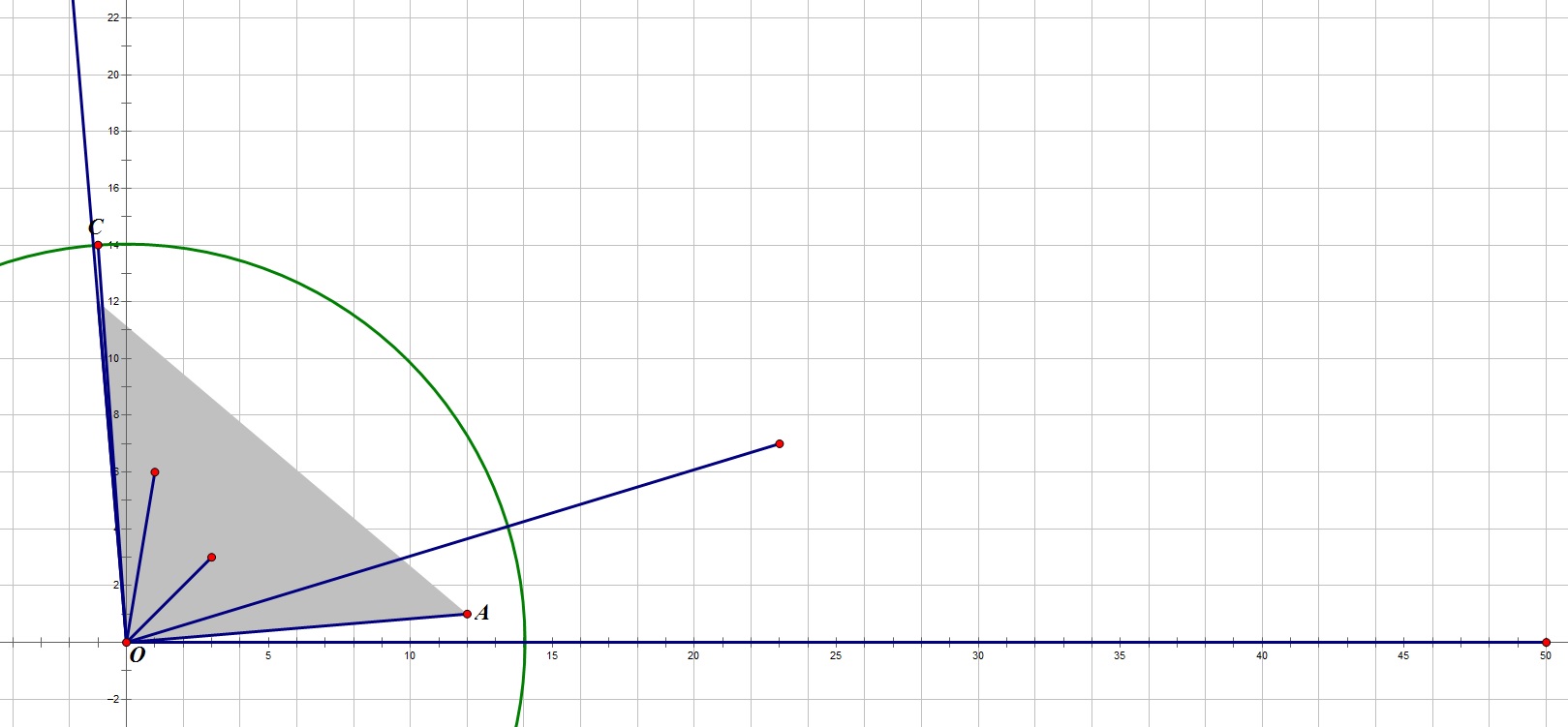
如图, 选择OC的长度做覆盖半径并让扇形的方向与灰色区域对齐即可
数据范围
$ 0 < m <= n <= 2*10^{5} $
$ 0 <= |x_i| , |y_i| <= 10^9$
子任务1:(80分)
$ 0 <= |x_i| , |y_i| <= 10^5$
子任务2:(160分)
无其他限制


